人工智能复习

人工智能复习

第一章 绪论

考点

  1. 人工智能的定义、概况；
  2. 人工智能主要学派及主要观点。

什么是人工智能？

需要先有信息、认识、知识、智力、智能概念才能定义人工智能。

  • 信息：是搭配了上下文的数据，是经过整理（解释）的数据，例如“今天天气是30摄氏度”，配合上下文（天气和摄氏度）形成了有意义的信息。
  • 认识：是用符号（例如文字）去整理信息，并且确定它们之间的联系。
  • 知识：是被认识了的信息和信息之间的联系。是经过加工（整理）的信息，例如“水在摄氏度0度以下会结冰”就是一种知识。
  • 智力：是学习的能力、解决问题的能力，强调运用推理来应对问题。
  • 智能：定义为知识集 + 智力。所以智能就是运用知识来解决问题的能力。

人工智能定义：就是利用机器去模仿人类的智能来解决问题。

人工智能学派及主要观点

符号主义学派（数理逻辑）

  • 主要观点：人工智能源于数理逻辑。认知基元是符号，以归结原理为基础。
  • 应用：IBM提出的DEEP BLUE国际象棋和WATSON认知系统。

联结主义学派（仿生学）

  • 主要观念：人工智能源于仿生学。通过神经元连接和相互作用模拟大脑的结构和功能，通过神经网络来实现智能行为。
  • 应用：计算机视觉、卷积神经网络、自然语言处理。

行为主义学派（控制论）

  • 主要观念：人工智能来源于控制论和反馈机制。通过模拟生物体在环境中的适应能力和行为来实现智能。
  • 应用：强化学习、Google研发的机器狗。

第二章 知识表示和推理

考点

  1. 命题逻辑语法、语义；

  2. 谓词逻辑语法、语义；

  3. 谓词推理规则（等价式、永真蕴含式）以及应用；

  4. 命题及谓词逻辑归结推理（子句、子句集、置换与合一、答案提取）。

谓词逻辑

  • 项
    1. 常数（Constant）：表示特定的对象，例如a、b、c。
    2. 变量（Variable）：表示可以取不同值的对象，例如x、y、z。
  • 谓词
    1. 谓词符号通常是大写字母，例如P(x)、Q(a,b)。
  • 量词
    1. 全称量词（Universal Quantifier）：表示对所有的情况都成立，符号为∀，例如∀x P(x)表示“对所有x，P(x)都成立”。
    2. 存在量词（Existential Quantifier）：表示存在某种情况成立，符号为∃，例如∃x P(x)表示“存在某个x，使得P(x)成立”。

谓词逻辑推理规则

  • 假言推理：

    P→Q, P ⇒ Q

  • 假言否定:

    P→Q, ¬Q ⇒ ¬P

  • 等等

谓词逻辑应用

  • 课件一中有两题例子，可以刷下。

归结推理

需要先了解反证法、子句集、归结操作的概念才能清楚归结推理。

  • 反证法

    P ⇒ Q 当且仅当 P ∧ ¬Q ⇔ False

  • 子句集

    1. 文字：原子公式及其否定。例如：P：正文字，¬P：负文字。
    2. 子句：任何文字的析取，当然一个文字自己也是子句。例如：P ∨ Q ∨ R。
    3. 子句集：子句的合取集合。例如 {P ∨ Q, ¬P ∨ R, ¬Q}这个子句集合表示了一个包含三个子句的集合，其中 P ∨ Q, ¬P ∨ R, 和 ¬Q 是各自的子句。在归结推理中，我们可以通过归结操作来处理这些子句，从而推导出新的子句或证明目标。

  • 归结操作

    1. 定义：归结操作步骤包括选择两个子句并尝试将它们合并成一个新的子句。合并的过程依赖于通过消解相反的文字来生成新的子句。
    2. 例子：有两个子句{P ∨ Q, ¬Q}，经过归结操作后生成新子句{P}。

归结推理的基本步骤是利用反证法：首先将目标子句的否定加入子句集中，然后通过归结操作处理子句集，直到推导出空子句。根据反证法的原理，这表明目标子句是可证明的。

  • 谓词公式转换子句集

    1. 消去蕴涵和等价符号
    2. 内移否定符号¬
    3. 变量标准化（变量换名）
    4. 消去存在量词（Skolemize）
    5. 化为前束型
    6. 把母式化成合取范式
    7. 略去全称量词
    8. 把母式用子句集表示
    9. 子句变量标准化（最好每个子句的变量都不一样）

  • 合一

    1. 定义：在谓词归结过程中（子句集内）寻找谓词相同但是项不同，把它们不同的项经过置换，使得该谓词项相同，就是合一。

  • 置换

    1. 定义：用σ = {v1/t1, v2/t2,…, vn/tn}来表示任一置换。vi /ti 是指表达式中的变量vi以项ti来替换，且不允许vi 用与vi 有关的项ti（但是ti中可以包含其它变量）作置换。

    2. 例子：{a/x, w/y, f(s)/z}是置换; {x/x}, {y/f(x)}不是置换;、

    3. 置换是同时进行的。

  • 复合置换

    1. 过程：θ={t1/x1,…,tn/xn}，λ={u1/y1,…,um/ym},求θ°λ
      1. 构成{t1λ/x1,…,tnλ/xn,u1/y1,…,um/ym};（可想象成先置换t1λ/x1,…,tnλ/xn这一部分再一个一个置换λ）
      2. 如果yj∈(x1,…,xn), 则删除uj/yj;（即替换的变量前面已经被换过了）（要记得是θ先做变换的，只要是θ里面更换的变量，λ都要删除）
      3. 如果tkλ=xk, 则删除tkλ/xk;（类似 y / y这种）
    2. 性质：(θ° λ)° μ=θ° (λ° μ) 成立，θ° λ=λ ° θ 不一定成立。

  • 最一般合一项（MGU）算法：

    给定两个原子公式 f 和 g：

    1. 初始化：

      σ={ };S={f,g}

      σ 是当前的替换集，初始为空。 S 是包含两个公式 f 和 g 的集合。

    2. 检查 S 是否包含相同的一对公式。如果是，停止并返回 σ 作为 f 和 g 的 MGU。

    3. 否则，找到 S 中不一致的项集 D={e1,e2}。

    4. 检查不一致的项：

      • 如果 e1=V 是一个变量，并且 e2 是不包含 V 的项（反之亦然），则更新替换集： σ=σ ° {V=t};S=S ° {V=t}。

    5. 否则，停止，表示 f 和 g 不能被合一。1

  • 应用归结原理求解问题

    1. 就是把待求解的问题否定加上与A(x)析取转换成子句并加入到子句集合中，运用归结操作求解答案。

第三章 搜索技术

考点

  1. 盲目搜索（深度搜索、宽度搜索、迭代加深搜索）；
  2. 启发式搜索（最好优先搜索、A*搜索）；
  3. 博弈树搜索（极大极小过程、alpha-beta剪枝）。

搜索的形式化定义

  1. 状态空间：即整个要搜索的空间。
  2. 动作：即在当前这个状态需执行的动作。
  3. 初始状态：就是自己目前的状态。
  4. 目标状态：目标的状态。
  5. 启发式函数：指导搜索的方向。

除此之外，搜索算法还包括后继函数、动作成本以及如何选择下一步动作（这个最重要）等等。

盲目搜索（无信息搜索）

采用固定的选择策略来选择下一个状态。

宽度优先搜索

  1. 定义：把当前要扩展的状态的后继状态放在边界的最后。
  2. 性质：宽度优先搜索具有完备性和最优性。
    • 完备性：宽度优先从短到长从上到下慢慢搜索，最终一定能找到目标状态。
    • 最优性：根据宽度优先搜索定义，短的路径一定会在长的路径前被探索完，所以一定有最优性。
    • 时空复杂度：时空复杂度开销很大，都是O(b^{d+1})，特别是空间复杂度。

深度优先搜索

  1. 定义：把当前要扩展的状态的后继状态放在边界的最前面。
  2. 性质：深度优先搜索不具有完备性和最优性。
    • 完备性：如果状态空间无限或者存在回路则找不到目标状态；若状态空间有限并且一直进行剪枝的话具有完备性。
    • 时空复杂度：时间复杂度为O(b^m)，空间复杂度O(bm)。

迭代加深搜索

其实就是深度优先和宽度优先缝合；具有宽度优先的优势（每个节点都搜索），也具有深度优先的优势（搜索快）

  1. 定义：迭代加深搜索从深度限制为0开始，逐渐增加深度限制，直到找到目标节点或搜索完整个图。每次搜索都是深度优先搜索，但只允许到当前的最大深度限制为止。
  2. 性质：具有完备性和最优性。
    • 完备性：类似宽度优先一样。
    • 最优性：类似宽度优先一样。
    • 时空复杂度：空间复杂度为O(b^{d})（跟宽度优先一样，可是不用提前存储下一层的节点）；时间复杂度为O(bm)（跟深度优先一样）。

启发式搜索

对于一个具体问题，构造专用于该领域的启发式函数 ℎ(𝑛), 该函数用于估计从节点𝑛到达目标节点的成本。要求对于所有满足目标条件的节点𝑛，有ℎ(𝑛) = 0。并且使用**评价函数f(n)**来选择下个要到达的状态。f(n) = g(n) + h(n)

  • g(n)是初始节点到n的实际代价。

贪婪最佳优先搜索

  1. 定义：就是利用启发式函数ℎ(n) 来对边界上的节点进行排序，然后每次选择**ℎ(n)**最小的节点n去搜索。
  2. 评价函数（可以理解成）：f(n) = h(n)
  3. 性质：没有完备性和最优性。

A*算法

  1. 定义：就是利用评价函数f(n) 来对边界上的节点进行排序，然后每次选择f**(n)**最小的节点n去搜索。

  2. 评价函数：f(n) = g(n) + h(n)

    • 启发式函数**h(n)*可采纳性：假设ℎ*(𝑛) 是从节点𝑛到目标节点的最优路径的成本，当对于所有节点𝑛，满足ℎ(𝑛) ≤ ℎ(𝑛)，ℎ(n)是可采纳的。
      • 为什么叫可采纳，是因为一直低估了最优的代价，可以让A*算法更好的找到最优解。
    • 启发式函数**h(n)**一致性：对于任意节点𝑛1和𝑛2，若 ℎ(𝑛1) ≤ 𝑐(𝑛1 → 𝑛2) + ℎ(𝑛2) 则ℎ(𝑛)具有一致性。
      • 为什么叫一致性，因为保证f值是非递减的。image-20240702224627410
    • 证明：一致性可推可采纳性：
      1. 假设启发式函数 h(n)是一致的。
      2. 假设 h(n) 不是可采纳的。这意味着存在某个节点 n 使得 h(n)>h∗(n)。
      3. 选择一个实际从起始节点 s 到目标节点的最优路径，并设这个路径为 s,n1,n2,…,ng，其中 ng 是目标节点。
      4. 在这条路径上，由于 h 是一致的，我们有： image-20240702223842521
      5. 由于目标节点 ng 的启发值为零（即 h(ng)=0），将这些不等式相加得到： image-20240702223905637
      6. 因为 c(s,ng)c(s, n_g)c(s,ng) 就是从 sss 到 ngn_gng 的最小实际代价 h∗(s)h^*(s)h∗(s)，所以： h(s)≤h∗(s)
      7. 这与假设的 h(s)>h∗(s) 矛盾。因此，假设 h(n) 不是可采纳的前提是错误的。

  3. 性质：可能具有最优性。

    • 一致性可以推出可采纳性。

    • 如果**h(n)**只具有可采纳性，没有环检测的情况下是有最优性的。有环检测则不是。

    • 如果**h(n)**具有一致性，就算有环检测，也有最优性。

博弈树搜索

Minimax算法

  1. 定义：假设对方能总是做出最优的行动，己方总是做出能最小化对方获得的收益的行动，通过最小化对方的收益，可以最大化己方的收益。
  2. 使用深度优先搜索。（模拟算法很重要）

剪枝

只要计算节点n的一部分子节点就可以确定在MiniMax算法中我们不会考虑走到节点n了；如果已经确定节点n不会被考虑，那么也就不用继续计算n的子节点了。如下图：x和y已经不用被搜索了。image-20240621191942772

  • MAX剪枝：对于Max节点n，如果它的α(子) ≥ β(父)的时候，就可以停止遍历n的子节点了。image-20240621192426769
  • MIN剪枝：对于Min节点n，如果它的α(父) ≥ β(子)的时候，就可以停止遍历n的子节点了。image-20240621192631831

简单来说，对于Min节点n, 如果β值变得 ≤ 某个Max 祖先节点的α值, 那么就可以停止扩展n节点了。Max节点也是一样的。

要记得！是α ≥ β就可以发生剪枝！

第四章 高级搜索

考点

  1. 爬山法（基本思想）；
  2. 遗传算法（基本操作）（旅行商问题）。

爬山法（基本思想）

  • 是一种贪婪局部搜索算法。 能很快朝着解的方向进展。
  • 登高：一直向值增加的方向持续移动，将会在到达一个 “峰顶”时终止，并且在相邻状态中没有比它更高的值。 这个算法保留搜索得路径，因此当前节点的数据结构只需要记录当前状态和它的目标函数值。
  • 优点：
    1. 它们只用很少的内存。（因为没有保留搜索得路径）
    2. 它们通常能在很大状态空间中找到合理的解。
  • 可以把爬山法想象成一种地形图，既有“位置”（用状态定义），又有“高度”（用启发式函数定义）。image-20240621202221480
  • 爬山法的缺点：容易陷入局部最优解。
    1. 局部最大值：局部极大值是一个比它的每个邻居状态都高的峰顶，但是比全局最大值要低。爬山法找不到最优解。
    2. 山脊：就是一系列的局部最大值，爬山法搜索容易陷入死循环。
    3. 高原：高原是在状态空间地形图上评价函数值平坦的一块区域。像上图的shoulder（山肩）和flat local maximum（水平的局部最大值）都是高原。爬山法搜索效率降低。
  • 解决优点：从不同的状态开始运行爬山法看看哪个解更好。

爬山法和模拟退火的区别

因为爬山法是局部贪婪算法，所以容易陷入局部最优解；模拟退火算法是全局优化算法，它可以接受比当前更差的解，所以不会容易陷入局部最优解，并且随着时间慢慢降低接受差解的概率。

模拟退火

三函数两准则(状态生成函数 状态接受函数 降温函数 退火结束准则 内循环终止准则)

流程图：image-20240703143135428

image-20240703144219931

遗传算法（基本操作）

遗传算法的一般步骤为image-20240621213314264

流程中，不一定每个个体都会发生交叉和变异，都是有概率的。

包括编码、适应度函数、选择、交叉、变异。(后面三种为基本操作)

  • 编码：就是将每个个体进行二进制编码。

  • 适应度函数：返回值是判断该个体的适应度，适应度越大代表该个体越好。

  • 选择：选择是用来确定重组或交叉个体，以及被选个体将产生多少个子代个体。适应度越大的个体被选择的概率越大。选择方法有：

    1. 轮盘赌：首先按照适应度比例分配给每个个体被选中的概率，然后所有个体被选中概率之和为1，再随机[0,1]生成浮点数，看落在哪个区间，就选择哪个个体。image-20240621212351847
    2. 锦标赛选择：就是按照轮盘赌抽几个个体进行适应度比较，适应度高的个体被选择，一直重复执行下去。

  • 交叉：结合父代中选择的个体中的信息而产生新的个体。交叉方法有：

    1. 单点交叉：在个体串中随机设定一个交叉点，实行交叉时，该点前或后的两个个体的部分结构进行互换，并生成两个新的个体。image-20240621213039839
    2. 两点交叉：随机设置两个交叉点，将两个交叉点之间的码串相互交换。

  • 变异：子代基因按小概率扰动产生的变化。变异方法有：

    1. 位点变异：群体中的个体码串，随机挑选一个或多个基因座，并 对这些基因座的基因值以变异概率作变动。image-20240621213549835

  • 遗传算法的特点：遗传搜索是针对一组候选解决方案（individuals）而不是单个候选方案进行的。在搜索过程中，算法会保留当前一代的一组个体。遗传算法的每次迭代都会创建下一代个体。相反，大多数其他搜索算法都维持单个解决方案，并迭代地修改它以寻找最佳解决方案。例如，梯度下降算法沿当前最陡下降方向迭代移动当前解，梯度方向为给定函数的梯度的负数。

  • 遗传算法的群体初始化规模：太小会导致局部最优解，太大会难以收敛。

  • 例子：TSP旅行商问题、背包问题

第五章 不确定知识表示以及推理

考点

  1. 贝叶斯网络定义及表示、联合概率表示、构建方法、朴素贝叶斯方法、独立性判断D分离；
  2. 贝叶斯网络边缘概率及条件概率计算。

贝叶斯网络定义及表示

  • 定义：它由一个有向无环图（表达了变量之间的有向依赖关系）和一系列条件概率表（衡量了上述关系的强度）组成。image-20240623174719759
  • 补充：P(e)可推出P(e)（一个参数），需要知道P(c|e)和P(c|e)可推出P(c|e)和P(c|~e)（两个参数）。以此类推。
  • 贝叶斯网络的构建：
    1. 在某种变量顺序下，对所有变量的联合概率应用链式 法则 Pr(X1,…,Xn) = Pr(Xn|X1,…, Xn-1)Pr(Xn-1|X1,…, Xn-2)…Pr(X1)
    2. 对于每个变量Xi ，考虑该变量的条件集合X1,…,Xi-1，Xi 和Xj 是条件独立的，则将Xj 从Xi 的 条件集合中删除。经过这一步骤，可以得到下式 Pr(X1,…,Xn) = Pr(Xn|Par(Xn))Pr(Xn-1|Par(Xn-1))…Pr(X1)。
    3. 基于上述公式，构建一个有向无环图。其中，对于每个用节点表示的变量Xi，其父节点为Par(Xi)中的变量集合。
    4. 为每个家庭（即变量及其父节点集合）确定条件概率表的取值。

朴素贝叶斯方法（上网找些题目看看）

  • 定义：就是人为定义条件独立的变量，使得式子变得更加简单。即类似P(A,B,C,D) = P(A|B)P(C|B)P(D|B)。image-20240623180235338
  • 就是先算给定x向量情况下y为正的可能性和y为负的可能性。

轻松搞定朴素贝叶斯(有例题)_朴素贝叶斯算法例题-CSDN博客这个讲的挺好的。

条件概率

  • 极大似然法：就是先把式子列出来，然后对数，再对该式子求导并且等于0。image-20240623180513734

贝叶斯网络的D-分离

  • 串形连接： 在串行连接中A通过事件B影响C，同样事件C也是用过事件B影响A。我们认为当证据B确定时，A、C条件独立。image-20200112230651132.png

  • 共同的原因：给定父节点的前提下，子节点们条件独立。image-20200112231016234.png

  • 共同的作用：当不给定子节点时，父节点们条件独立。image-20200112231325308.png

  • 若存在一条路径将这两个节点（直接）连通，则称这两个节点是相关的。若不存在这样的路径将这两个节 点连通，则这两个节点就是独立的。

贝叶斯网络计算

  • 就是一直使用加法原理把父节点加入到式子中，然后链式法则，再对式子展开（条件独立就可以删除）。image-20240623181434174

第七章 机器学习

考点

  1. 监督学习（分类与回归，感知机、逻辑回归；神经网络、反向传播、CNN、RNN）；
  2. 非监督学习（Kmeans）；
  3. 强化学习（MDP定义、状态值函数和动作值函数、Q学习及SARSA、DQN）。

有监督学习

  • 定义：会给定输入特征和输出的标签（Y）

分类

  • 定义：预测离散型变量。给定(x1, y1), (x2, y2), …, (xn, yn)，学习一个输入x、预测y的函数f(x)。y是离散的。image-20240623195838671

回归

  • 定义：预测连续性变量。给定(x1, y1), (x2, y2), …, (xn, yn)，学习 一个输入x、预测y的函数f(x) 。y是连续的。image-20240623200254815

联结主义（Connetionism）学派：认为人工智能源于仿生学。（神经网络）

感知机学习

解决二分类问题的算法。是有监督学习中的分类。

  • 定义：主要是处理线性可分的数据。对于拥有d个特征的 x=(x1,x2,…,xd) , 计算它的带权“分数” 。如果分数大于0则预测为真，分数小于0则预测为假。

  • 输入层：感知机接收一组输入特征向量 x=(x1,x2,…,xn)，每个输入有一个对应的权重 w=(w1,w2,…,wm)。

  • 加权求和：输入特征向量和权重向量进行加权求和，计算公式为：

    \begin{equation} z = \mathbf{w} \cdot \mathbf{x} + b = \sum_{i=1}^{n} w_i x_i + b \end{equation}

    其中，b是偏置。

  • 激活函数：加权求和的结果通过激活函数（通常是阶跃函数）进行处理，输出一个二值结果。阶跃函数的定义为：

    f(z)={1if z≥00if z<0f(z) = \begin{cases} 1 & \text{if } z \geq 0 \\ 0 & \text{if } z < 0 \end{cases}

  • 损失函数：定义为所有误分类点到分类线距离的总和。（M是所有误分类点的集合）

    L(w,b)=−∑xi∈Myi(w⋅xi+b)L(w, b) = -\sum_{\mathbf{x}_i \in M} y_i (w \cdot \mathbf{x}_i + b)

    修改函数利用梯度下降法：

    \begin{align} \nabla_w L(w,b) &= -\sum_{\mathbf{x}_i \in M} y_i \mathbf{x}_i \\ \nabla_b L(w,b) &= -\sum_{\mathbf{x}_i \in M} y_i \end{align}

  • 感知机学习：

    1. 先初始化权重向量w(0)和偏置b , 然后根据D来修正w和b。（通常初始化为0）

    2. 对于每个训练样本，计算感知机的输出。

    3. 如果感知机某个样本的输出与真实标签不一致，根据以下规则更新权重和偏置：

      \begin{align} w_{i+1} &\leftarrow w_i + \eta y_i x_i \\ b &\leftarrow b + \eta y_i \end{align}

      其中η是学习率。

    4. 跳回第二步。

  • 分类图片如下：image-20240623210433383

逻辑回归

感知机算法只要计算的分数大于0输出标签为真，可是分数1和1000也是输出标签为真。

解决多分类的算法。

  • 定义：和感知机学习算法一样，主要处理线性可分的数据。对于拥有d个特征的 x=(x1,x2,…,xd) , 计算一个0到1的概率值，表示样本属于某个类别的概率。

  • 输入层：感知机接收一组输入特征向量 x=(x1,x2,…,xn)，每个输入有一个对应的权重 w=(w1,w2,…,wm)。gai

  • 加权求和：输入特征向量和权重向量进行加权求和，计算公式为：

    \begin{equation} y = \mathbf{w} \cdot \mathbf{x} + b = \sum_{i=1}^{n} w_i x_i + b \end{equation}

    其中，输出y是该样本属于这个类别的可能性（目前还未经过转化），b是偏置。

  • 激活函数：使用Logistic函数将求和y映射到一个介于 0 和 1 之间的概率值：

    σ(y)=11+e−y\sigma(y) = \frac{1}{1 + e^{-y}}

    这里的σ(y)是把刚刚加权求和的总数转换成概率。若y越大，则概率σ(y)就越大。

  • 损失函数：定义为交叉熵函数。

    L(w)=−∑i=1N[yilog⁡(qi)+(1−yi)log⁡(1−qi)]L(w) = -\sum_{i=1}^{N} \left[ y_i \log(q_i) + (1 - y_i) \log(1 - q_i) \right]

    yi 是第 i 个样本的真实标签（0或1），qi是模型预测的第 i 个样本属于类别 1 的概率。当qi越接近yi，损失函数值就越小。（等价于让损失函数最小）

    修改函数利用梯度下降法：

    \begin{align*} \nabla_{\mathbf{w}} L(\mathbf{w}) & = -\sum_{i=1}^{N} \left[ y_i - q_i \right] \mathbf{x}_i \end{align*}

  • 逻辑回归学习：

    1. 初始化w和偏置 b，通常可以选择为零或者随机初始化。

    2. 对于每个训练样本 (xi,yi)，计算模型的预测输出 qi=σ(w⋅xi+b)。

    3. 如果某个样本的输出与真实标签不一致，根据以下规则更新权重和偏置：

      w←w−η∑i=1N[qi−yi]xi\mathbf{w} \leftarrow \mathbf{w} - \eta \sum_{i=1}^{N} \left[ q_i - y_i \right]\mathbf{x}_i

    4. 跳回第二步。

  • 其实本质是二分类输出还是0和1，还是一条直线。

人工神经网络

单层神经网络
  • 定义：一个基本的神经网络包括：输入、计算、输出。下图是一个典型的人工神经网络模型，它包含3个输入，1个 输出，以及2个计算功能。image-20240624000843701
  • 人工神经元：人工神经网络中的计算单位。由下列部分组成：
    1. 输入信号xi
    2. 一个激活层对输入信号乘上加权求和，神经元的激活层由加权输入的总和确定。
    3. 一个阈值函数 f(x)，该函数通过确定激活是低于还是高于阈值来计算最终输出。
  • 应用：可以实现“与”、“或”功能，可是不能处理异或。image-20240624002553421
多层神经网络

优势：单层神经网络只能处理线性问题，而两层神经网络可以无限逼近任意连续函数。面对复杂的非线性分类任务，带一个隐藏层的两层神经网络可以分类的很好。输入和输出节点之间的附加层称为隐藏层。

原因：从输入层到隐藏层时， 数据发生了空间变换。这是因为输入层的阈值函数是非线性的，对数据进行了转换。

传递：训练的算法每次迭代都有前向传递阶段和反向传递阶段。

  1. 前向传递阶段：利用第(l)层处的神经元的输出来计算第(l+1)层的输出。
  2. 反向传递阶段：第(l+1)层的权重在更新第(l)层的权重之前被更新。

激活函数：

  1. 双曲正切函数(tanh)：

    \begin{align} \tanh(x) &= \frac{e^x - e^{-x}}{e^x + e^{-x}}\\ \tanh'(x) &= 1 - \tanh^2(x) \end{align}

  2. sigmoid函数：

    \begin{align} f(x) &= \frac{1}{1 + e^{-x}}\\ f'(x) &= f(x) \left(1 - f(x)\right) \end{align}

    函数的导数特性很重要！

损失函数：定义为最小二乘法：

E=12e2=12(T−O)2E = \frac{1}{2} e^2 = \frac{1}{2} (T - O)^2

为了使用梯度下降调整权重 wjk,我们首先计算在wjk 上误差E的偏导数：

\begin{align*} \frac{\partial E}{\partial w_{jk}} &= \frac{\partial E}{\partial e} \times \frac{\partial e}{\partial O_k} \times \frac{\partial O_k}{\partial w_{jk}} \\ &= -\left( e \right) \times \left( O_k (1 - O_k) \right) \times \left( O_j \right) \\ &= -(T_k - O_k) O_k (1 - O_k) O_j \end{align*}

image-20240624193053302

前向传播输入：

  • 净输入：image-20240624193550696
  • 净输出：image-20240624193620428

反向传播误差：

  • 对于输出层，定义误差为：image-20240624193737699
  • 对于隐藏层，定义误差为：image-20240624193803486
  • 权重更新公式（利用梯度下降）：image-20240624193903303
  • 缺点：很容易梯度消失，每传递一层梯度就是原本的0.25倍。
  • (´∇｀) 欢迎回来！ (cnblogs.com)把这题刷一下基本没问题了(更改偏置b1和b2的时候，这个偏置项有点特殊，可以看成是一个隐藏层的节点进行处理，o1和o2的Err值都对它影响）b9a535cdb2ab277d41473d468584db9

卷积神经网络(CNN)

  • 是深度学习算法。主要用于图像识别。

  • 卷积计算：如下图img

    描述卷积的四个量：卷积核个数、卷积核大小f、填充0值p、步长s。

    假设原本大小为拿，卷积结果大小为(n可以是高或者宽)

    n+2p−fs+1\frac{n + 2p - f}{s} + 1

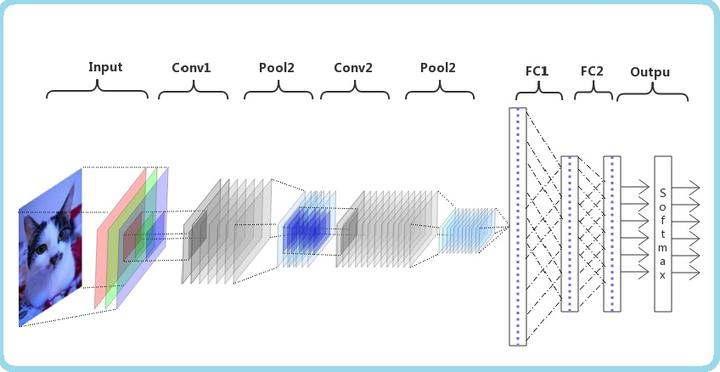
  • 卷积神经网络的构造

    1. 输入层：输入层接收原始图像数据。图像通常由三个颜色通道（红、绿、蓝）组成。（输入数据）

    2. 卷积层（可以有多层卷积层）：将输入图像与卷积核进行卷积，然后再进行非线性变换(RELU)，再进行池化。（提取特征）RELU函数为：

      ReLU(x)=max⁡(0,x)\text{ReLU}(x) = \max(0, x)

    3. 全连接层：全连接层将提取的特征映射转化为网络的最终输出。（就是多层神经网络）卷积神经网络（CNN）基础及经典模型介绍（续） - 知乎

    4. 输出层：输出层是CNN的最后一层，其神经元的数量等于分类任务中的类别数。输出层的激活函数根据任务的不同而选择，例如Softmax用于多分类任务，Sigmoid用于二分类任务。

  • 卷积神经网络（CNN）是一种深度学习方法，它的发展历史可以追溯到20世纪90年代。最早的CNN是由Yann LeCun等人提出的，他们利用多层感知机（MLP）进行手写数字识别。随着技术的进步，CNN的结构变得越来越复杂，性能也得到了显著提高。

  • 输入层用于接收原始数据，通常是图像数据。图像通常由三个颜色通道（红、绿、蓝）组成，每个通道包含图像的像素值。输入层只是数据的初始存储区域，不进行任何处理。

  • 卷积层是CNN的核心部分，主要用于提取输入数据的局部特征。卷积层通过在每个位置计算卷积核与输入数据的点积，卷积操作后，特征图通过激活函数进行非线性变换，这种非线性变换使模型能够学习和表示更复杂的特征。池化层用于对卷积层生成的特征图进行下采样，减少特征图的尺寸，从而降低计算复杂度。

  • 全连接层位于网络的最后几层，将前面层提取到的特征整合并映射到最终的输出。全连接层类似于传统的多层神经网络，每个神经元与上一层的所有神经元相连。通过全连接层，模型能够基于提取到的特征进行分类或回归任务。

  • 卷积神经网络和全连接神经网络区别：卷积神经网络有卷积层能够提取更多的数据特征，并且卷积的时候参数是共享的还有平移不变性。

循环神经网络（RNN）

  • 是深度学习算法，主要用于语言识别。

  • 因为其余的神经网络输出只和当前时刻网络的输入相关。可是像预测天气这种问题还是很需要之前的数据的。这是一个有记忆的神经网络。img

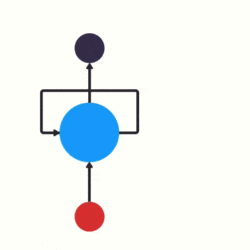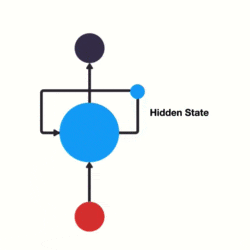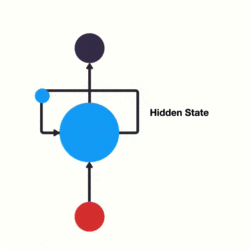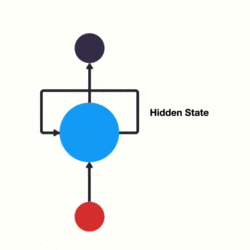
  • 例如像判断广州是目的地还是出发地，需要看前一个英文单词，所以需要用到之前的记忆。image-20240624215758219

  • 简单来说，就是隐藏层的输出还存储在记忆中，并且记忆内容作为隐藏层的输入。image-20240624214743675

  • 例子如下：假设所有权重都是1，激活函数都是线性的。

  • 第一步：image-20240624215015924

  • 第二步：image-20240624215128804

  • 第三步：image-20240624215206066

  • 不同的输入顺序会影响到循环神经网络的输出，因为是有记忆的！

基本上理解卷积神经网络就是眼睛，主要用来图像识别；循环神经网络就像嘴巴，主要用来语言识别。

无监督学习

就是不会给出标签的学习。

K-Means

  • 聚类：基于距离度量，将对象集合聚类到簇(cluster)中，使得簇内对象的距离尽量小，且簇之间对象的距离尽量大。

  • 向量x和y之间距离公式：

    1. 街区距离：

      d(x,y)=∑i=1n∣xi−yi∣d(x, y) = \sum_{i=1}^{n} |x_i - y_i|

      n是向量的维度。

    2. 欧式距离：

      d(x,y)=∑i=1n(xi−yi)2d(x, y) = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2}

      n是向量的维度。

  • K-Means算法流程：

    1. 初始化：
      • 确定聚类的数目K。
      • 随机选择K个数据点当作质心。
    2. 分配每个点到最近的质心：
      • 对于每个数据点，计算它到每个质心的距离。
      • 将每个数据点分配到距离最近的质心所属的簇。
    3. 更新质心：
      • 对于每个簇，计算所有属于该簇的数据点的平均值，这个平均值就是新的质心。
      • 更新质心的位置为新的平均值。
    4. 重复步骤2和步骤3：
      • 反复执行步骤2和步骤3，直到质心不再发生变化，或者达到预设的迭代次数。
    5. 完成聚类：
      • 最终的质心和数据点的分配结果即为K-means算法的输出。

  • K-Means算法改进：

    可以发现，一开始选择的质心很重要，很影响算法。所以初始化的质心应该离得越远越好。

    • K-Means++算法：

      1. 计算每个数据点x到最近的一个已选质心的距离

        对于每个数据点 x，计算它到最近的一个已选质心的距离D(x)。假设我们已经选择了m 个质心 c1,c2,…,cm。

        D(x)=min⁡i∈{1,2,…,m}dist(x,ci)D(x) = \min_{i \in \{1, 2, \ldots, m\}} \text{dist}(x, c_i)

      2. 计算每个点被选中当质心的概率

        将每个数据点 x 到最近质心的距离 D(x) 的平方作为该点被选为下一个质心的概率权重。具体来说，计算概率权重：

        P(x)=D(x)2∑y∈XD(y)2P(x) = \frac{D(x)^2}{\sum_{y \in X} D(y)^2}

      3. 轮盘赌选择下一个质心

        离被选中的质心越远被选做质心的可能性越大。

强化学习

强化学习基本要素有：状态、动作、策略、奖励、值函数（状态值函数、动作值函数）

强化学习的基本目标是：找到最大化奖励的策略。

  • 状态值函数V(s)：用于评断当前状态s在给定策略π下，未来累计的期望值。

    Vπ(s)=Eπ[∑t=0∞γtRt+1∣S0=s]V^{\pi}(s) = \mathbb{E}_{\pi} \left[ \sum_{t=0}^{\infty} \gamma^t R_{t+1} \mid S_0 = s \right]

    image-20240625155050199

    两条公式是等价的。

  • 动作值函数Q(s,a)：表示在状态 s 下采取动作 a，然后遵循策略 π 时，未来累积奖励的期望值。

Q-learning

是一种贪心算法，学习的策略和实际的策略可能不同。异策略。

通过反复的试验和更新，逐渐逼近最优的状态值函数（Q函数），从而找到最优策略。

更新Q值的公式如下：

Q(s,a)←r+γmax⁡a′Q(s′,a′)Q(s, a) \leftarrow r + \gamma \max_{a'} Q(s', a')

其中r是到达s’的奖励。

更新Q值时，因为是贪心算法，所以取s’状态的max值。

SARSA

学习的策略与实际执行的策略是一致的。同策略。

更新Q值的公式如下：

Q(s,a)←r+γQ(s′,a′)Q(s, a) \leftarrow r + \gamma Q(s', a')

更新Q值时，所以取s’状态的Q值。

Q-learning 和 SARSA区别

  1. 策略类型
    • Q-learning: Off-policy，学习的策略（最优策略）与执行的策略（探索策略）不同。
    • SARSA: On-policy，学习的策略与执行的策略相同。
  2. 更新Q值的依据
    • Q-learning: 更新Q值时使用的是新状态s’下的最大Q值（max⁡Q(s′,a′)）。
    • SARSA: 更新Q值时使用的是新状态s’下实际选择的动作的Q值（Q(s′,a′)）。

TD时序差分

更改Q值的时候，还会利用到原本的Q值。

  • 可以与Q-learning和SARSA混合使用。

  • Q-learning TD算法公式：

    Q(s,a)←(1−α)Q(s,a)+α[r+γmax⁡a′Q(s′,a′)]Q(s, a) \leftarrow (1 - \alpha)Q(s, a) + \alpha \left[ r + \gamma \max_{a'} Q(s', a') \right]

  • SARSA TD算法公式：

    Q(s,a)←(1−α)Q(s,a)+α[r+γQ(s′,a′)]Q(s, a) \leftarrow (1 - \alpha)Q(s, a) + \alpha \left[ r + \gamma Q(s', a') \right]

    α是学习率，γ是折扣因子。

DQN

是Q-learning算法和深度神经网络结合，并额外引入两个机制经验回放和目标网络。

  • 经验回放：将智能体探索环境得到的数据储存起来，然后随机采样小批次样本更新深度神经网络的参数。

  • 目标网络：额外引入一个目标网络（和Q网络具有同样的网络结构），此目标网络不更新梯度，每隔一段时间将Q网络的参数赋值给此目标网络。

  • 实现步骤：

    1. 初始化神经网络：包括主网络和目标网络的初始化。
    2. 与环境交互：使用当前策略（通常是 ε-greedy 策略）与环境交互，收集经验数据。
    3. 存储经验：将每次交互的经验（状态、动作、奖励、下一个状态）存储到经验回放缓冲区中。
    4. 经验回放：从经验回放缓冲区中随机抽取小批量的经验样本，用于训练主网络。
    5. Q-learning 更新：使用抽样的经验样本，计算 Q-learning 的目标并更新主网络的参数。
    6. 更新目标网络：定期更新目标网络的参数，以保持其与主网络的一致性，但更新频率较低，如每隔一定步数更新一次。
    7. 迭代训练：重复上述步骤直至收敛或达到预定的训练步数。

  • DQN和深度神经网络区别

    1. 概括

      • 深度神经网络是一种通用的机器学习模型，用于学习输入数据中的复杂模式和特征。
      • DQN 是一种强化学习算法，结合了深度神经网络和Q-learning的思想。

    2. 训练方法

    • 深度神经网络训练通常使用监督学习或无监督学习的方法，通过最小化预测输出与真实标签之间的损失来优化网络参数。
    • DQN训练过程是通过交互式学习与环境进行，智能体通过试错和反馈来优化动作值函数。

押题

谓词归结一题 贝叶斯网络一题 A*一题 Minimax剪枝一题 感觉爬山法可能会有一题

遗传一题

Qlearning一题

k-means一题

BP一题

人工智能复习
https://tobytam23.github.io/2024/12/02/人工智能复习/
Author
tanzhuoheng
Posted on
December 2, 2024
Licensed under